小学生の時に教えてもらった驚いた事
1から10まで全部足すと55
『1から10までの数を足していくと、いくつになる?』
『55でーす』
これは簡単です。
電卓でも、ソロバンでも、ひとつずつ足していけばすぐにできます。
『じゃあ、1から100までの数を足すといくつ?』
もー計算するのは面倒だ。
『じゃあ1から10000までは?』
無理、無理
そう思った時、小学校の先生が
教えてくれました。
簡単な計算方法
数字を最初から順に足していくのではなく
最初の数字と、最後の数字を足す。
次に最初から二番目の数字と、
最後から二番目の数字を足す。
するとその数は一緒になります。
その組み合わせが、全部の数の半分ある。
1から100までの場合
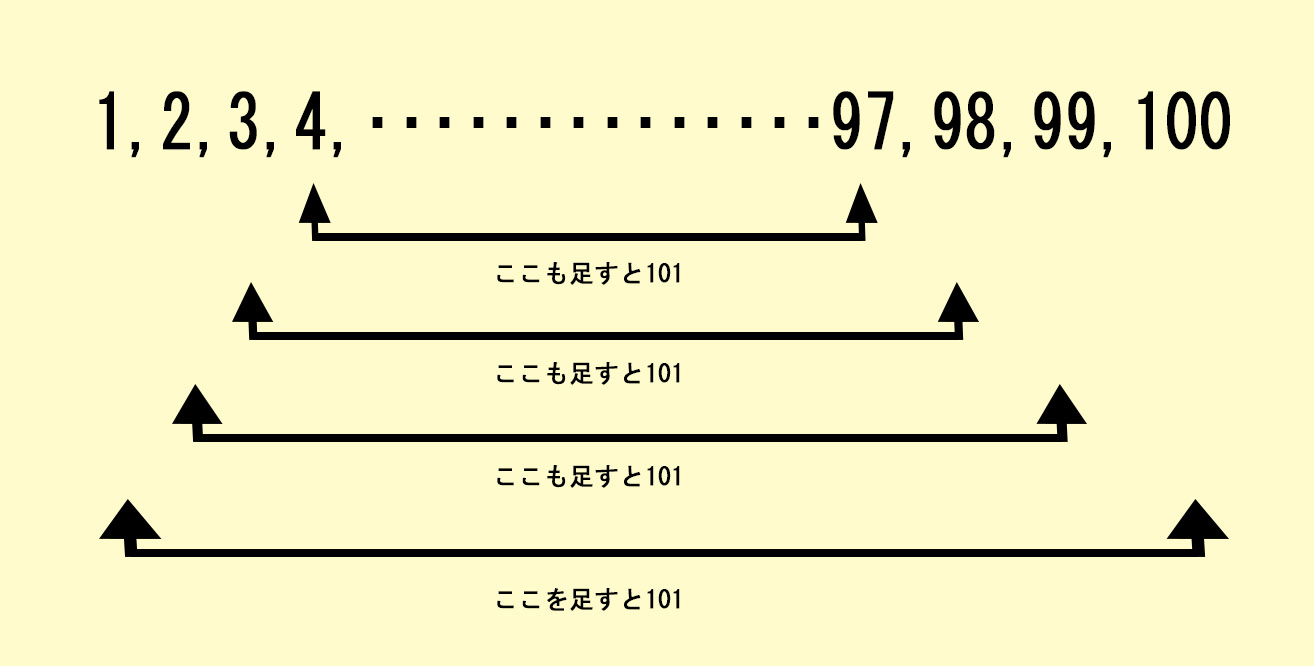
1、2、3、・・・・98、99、100
1+100=101
2+99=101
3+98=101
・
・
・
・
・
この101になる組み合わせが50個ある。
101*50=5,050
なるほど!
とても驚いたのです。
感動すら覚えました。
こんな計算方法があるんだと。
これがきっかけで算数が好きになったのかも
しれません。
足す数が奇数だった場合は?
足す数が奇数だったらどうするんだ?
最後の数だけ別にして後で足せばいいのか。
1から141の場合
最初に1から140まで足した数を計算し、 それに141を足す。
141*70+141=10,011
普通に考えれば簡単。
数式にすると
1からXまでを順に足した数を求める。
(1+X)*X÷2
となります。
この数式で奇数の数でも大丈夫です。

考え方を変える
1からXまで足すというので、
文字とおりそのまま足していくのではなく、
考え方を変えることによって、
同じ組み合わせのものがいくつもできる、
それをかけ算することによって簡単に
解けるという事がわかりました。
考え方、見方を変えると新しい発見ができます。
算数に限らず、難しい問題も
考え方、見方を変えると解決する事が
あるということです。
大変な事がある時も、いろいろな見方をしてみる。
客観的に見るとか、俯瞰で見るとかで
自分の持っている価値観とは違う目で 見ると、
新たな視点が生まれます。
私は小学校の時にこれで
算数って面白いなと思い好きになりました。
なにかを好きになる理由は
こんな小さい事から始まるのかもしれません。









